A Desigualdade de Cauchy-Schwarz é uma relação muito rica no contexto matematico, pois pode ser utilizado em diversas áreas, tais como em álgebra linear aplicando-se a vetores, em análise aplicando-se a séries infinitas e integração de produtos, e na teoria de probabilidades aplicando-se as variâncias e covariâncias.
Definição: Para quaisquer 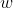 e
e 
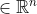 , tem-se
, tem-se 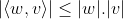 .Onde a igualdade é valida se, e somente se, uns dos vetores
.Onde a igualdade é valida se, e somente se, uns dos vetores 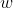 ,
,  é multiplo do outro.
é multiplo do outro.
Demonstração: seja dado dois vetores quaisquer 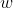 e
e  , onde
, onde 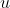 é o vetor projeção e
é o vetor projeção e  é o vetor que vai do extremo do vetor
é o vetor que vai do extremo do vetor 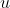 até o extremo do vetor
até o extremo do vetor 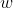 , então temos:
, então temos:
Então para qualquer vetor
Então:


Como posso provar que a desigualdade de Cauchy-Schwarz vale apenas quando os vetores são linearmente dependentes?
ResponderExcluir