Cálculo da área de uma superfície fechada

Olá, hoje vamos ver uma igualdade bem interessante do calculo vetorial, partindo do terorema da divergência, chegaremos a uma formula alternativa para o calculo da área de uma superfície fechada .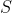

TEOREMA DA DIVERGÊNCIA: Seja 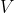uma região solida simples e seja 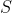a superfície fronteira de 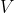, com 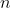um vetor normal unitário exterior a superficie 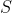. E seja 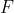um campo vetorial cujas funções componentes tem derivadas parcias continuas em uma região aberta que contenha 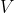. Então:

                                                

Onde:

*O teorema da divergência é algumas vezes chamado de teorema de Gauss, em homenagem ao grande matemático alemão Carl Friedrich Gauss que descobriu esse teorema durante suas pesquisas sobre eletrostática. Em muitos países da europa, o teorema da divergência é conhecido como Teorema de Ostrogradsky, em homenagem ao matemático russo Mikhail Ostrogradski que publicou esse resultado em 1826.

Da relação:

 

temos que se o campo for igual ao vetor normal, ou seja , ,então:

 

Porém, como 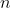é um vetor normal unitário, temos que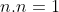

E então:

 

Vamos utilizar essa formula para o calculo da área da superfície da esfera :

Esfera:

O vetor normal unitário é dado por:

E então:

utilizando a formula ,temos que :

portanto, a área da esfera é dada por:

onde 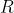é o raio.