Dedução das formulas do movimento de projéteis

   Quando atiramos um projétil ao ar, geralmente queremos saber de antemão que distância percorrerá (alcançará o alvo?), que altura alcançará (passará cobre a elevação?) e quando aterrissará (quando obteremos os resultados?)Conseguimos essas informações a partir da direção, do sentido e do módulo do vetor velocidade inicial, usando a segunda lei de Newton para o movimento.

                Figura 1

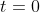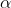Assumindo que o projétil é lançado a partir da origem no instante no primeiro quadrante com velocidade inicial (Figura 1). Se fizer um ângulo com a horizontal, então 

Se usarmos a notação mais simples para o módulo da velocidade inicial , então

A posição inicial do projétil é

A segunda lei de Newton para o movimento diz que a força que atua sobre um projétil é igual à massa 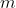do projétil vezes sua aceleração, ou , se  for o vetor posição do projétil e 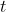 for o tempo. Se a força for somente a força gravitacional , então

Encontramos como uma função de ao resolvermos o problema de valor inicial.

Equação diferencial:

considerações iniciais:      e quando

A primeira integração dá

Uma segunda integração dá

Substutuindo os valores de e das equações  1 e 2, temos

ou

A equação [3] é a equação vetorial para o movimento ideal do projétil. O ângulo 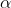 é o ângulo de lançamento(ângulo de tiro, ângulo de elevação) do projétil e , como dissemosanteriormente, é o módulo da velocidade inicial do projétil.

As composições de  dão

Onde  é a distância na horizontal da base de lançamento e  é a altura do projétil no instante